Page 137 - 《广西植物》2025年第4期

４ 期 郁书君等: 三角梅品种的表型遗传多样性综合分析与评价 ７ ５ １

分ꎬ累计贡献率达 ７８.６８９％(表 １０)ꎬ可以代表三角
梅性状的绝大部分信息ꎬ其中特征值表示主成分
影响力度的大小ꎬ贡献率表示主成分对原始变量

即三角梅性状的解释程度ꎮ

表 １０ 各主成分特征值与贡献率
Ｔａｂｌｅ １０ Ｅｉｇｅｎｖａｌｕｅｓ ａｎｄ ｃｏｎｔｒｉｂｕｔｉｏｎ ｒａｔｅｓ
ｏｆ ｅａｃｈ ｐｒｉｎｃｉｐａｌ ｃｏｍｐｏｎｅｎｔ
累计贡献率
主成分 贡献率
特征值 Ｃｕｍｕｌａｔｉｖｅ
Ｐｒｉｎｃｉｐａｌ Ｃｏｎｔｒｉｂｕｔｉｏｎ
Ｅｉｇｅｎｖａｌｕｅ ｃｏｎｔｒｉｂｕｔｉｏｎ
ｃｏｍｐｏｎｅｎｔ ｒａｔｅ (％)
ｒａｔｅ (％)
１ ２.８６９ １４.３４６ １４.３４６
２ ２.２７７ １１.３８３ ２５.７２９
３ １.９９１ ９.９５７ ３５.６８６
４ １.９４２ ９.７０９ ４５.３９５
５ １.８３５ ９.１７４ ５４.５６９
６ １.８２８ ９.１４２ ６３.７１１
∗表示显 著 相 关 ( Ｐ < ０. ０５)ꎻ ∗∗ 表 示 极 显 著 相 关 ( Ｐ < ７ １.７２０ ８.６００ ７２.３１０
０.０１)ꎮ
８ １.２７６ ６.３７９ ７８.６８９
∗ｉｎｄｉｃａｔｅｓ ｓｉｇｎｉｆｉｃａｎｔ ｃｏｒｒｅｌａｔｉｏｎ ( Ｐ < ０. ０５)ꎻ ∗∗ ｉｎｄｉｃａｔｅｓ
ｅｘｔｒｅｍｅｌｙ ｓｉｇｎｉｆｉｃａｎｔ ｃｏｒｒｅｌａｔｉｏｎ (Ｐ<０.０１).
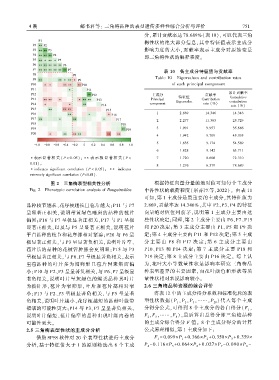
图 ２ 三角梅表型相关性分析 根据特征向量分量的绝对值可知每个主成分
Ｆｉｇ. ２ Ｐｈｅｎｏｔｙｐｉｃ ｃｏｒｒｅｌａｔｉｏｎ ａｎａｌｙｓｉｓ ｏｆ Ｂｏｕｇａｉｎｖｉｌｌｅａ 中各性状的载荷程度( 宗亦臣等ꎬ２０２２)ꎮ 由表 １１
可知ꎬ第 １ 主成分是最重要的主成分ꎬ其特征值为
品种枝节越长、花序梗越长且苞片越大ꎻＰ１１ 与 Ｐ７ ２.８６９ꎬ贡献率达 １４.３４６％ꎬ其中 Ｐ２、Ｐ３、Ｐ４ 的特征
呈显著正相关ꎬ说明带黄绿色暗斑的品种的苞片 向量绝对值位列前茅ꎬ说明第 １ 主成分主要由这
偏圆ꎻＰ１６ 与 Ｐ７ 呈极显著正相关ꎬＰ１７ 与 Ｐ１ 呈极 些性状决定ꎻ同理ꎬ第 ２ 主成分主要由 Ｐ６、Ｐ７、Ｐ１５
显著正相关ꎬ以及与 Ｐ５ 呈显著正相关ꎬ说明苞片 和 Ｐ２０ 决定ꎻ第 ３ 主成分主要由 Ｐ１、Ｐ５ 和 Ｐ９ 决
平直品种的枝节和花序都相对紧凑ꎻＰ２０ 与 Ｐ６ 呈 定ꎻ第 ４ 主成分主要由 Ｐ１１ 和 Ｐ１２ 决定ꎻ第 ５ 主成
极显著正相关ꎬ与 Ｐ３ 呈显著负相关ꎬ说明叶片窄、 分 主 要 由 Ｐ８ 和 Ｐ１７ 决 定ꎻ 第 ６ 主 成 分 主 要 由
苞片长的品种的花被管肿胀会更明显ꎻＰ１５ 与 Ｐ３ Ｐ１０、 Ｐ１３ 和 Ｐ１４ 决 定ꎻ 第 ７ 主 成 分 主 要 Ｐ１８ 和
呈极显著正相关ꎬ与 Ｐ６、Ｐ７ 呈极显著负相关ꎬ表示 Ｐ１９ 决定ꎻ第 ８ 主成分主要由 Ｐ１６ 决定ꎮ 综上认
重苞品种的叶片多为阔卵形且苞片因聚集而偏 为ꎬ花叶大小等数量性状是影响本研究三角梅品
小ꎻＰ１０ 与 Ｐ２、Ｐ３ 呈显著负相关ꎬ与 Ｐ６、Ｐ７ 呈极显 种表型差异的主要因素ꎬ而花叶颜色和形状等质
著负相关ꎬ说明叶片呈灰绿色的蝶类品种其叶片 量性状相对来说影响较小ꎮ
为披针形ꎬ苞片为窄卵形ꎬ叶片和苞片都相对窄 ２.６ 三角梅品种资源的综合评价
小ꎻＰ１３ 与 Ｐ２、Ｐ３ 呈极显著负相关ꎬ与 Ｐ５ 呈显著 将表 １２ 中的主成分得分系数和标准化后的表
负相关ꎬ说明叶片越小、花序梗越短的品种叶缘带 型性状数据( Ｐ ꎬＰ ꎬＰ ꎬꎬＰ ) 代入每个主成
３
２０
１
２
褶皱的可能性更大ꎻＰ１４ 与 Ｐ３、Ｐ７ 呈显著负相关ꎬ 分得分公式ꎬ可得到 ８ 个主成分的各自得分( Ｆ ꎬ
１
说明叶片偏短、苞片偏窄的品种出现叶缘内卷的 Ｆ ꎬＦ ꎬꎬＦ )ꎬ最后算出总得分即三角梅品种
８
３
２
的主成分综合得分 Ｆ 值ꎮ ８ 个主成分得分的计算
可能性更大ꎮ
２.５ 三角梅表型性状的主成分分析 公式原理相似ꎬ第 １ 主成分如下:
借助 ＳＰＳＳ 软件对 ２０ 个表型性状进行主成分 Ｆ ＝ ０.０９９×Ｐ ＋ ０.３６６ ×Ｐ ＋ ０.３５０ ×Ｐ ＋ ０.３５９ ×
２
３
１
１
分析ꎬ基于特征值大于 １ 的原则筛选出 ８ 个主成 Ｐ －０.１１６×Ｐ ＋０.０６４×Ｐ ＋０.０２７×Ｐ －０.０９０ ×Ｐ －
８
４
５
７
６