Page 118 - 《广西植物》2024年第10期
P. 118
1 9 2 0 广 西 植 物 44 卷
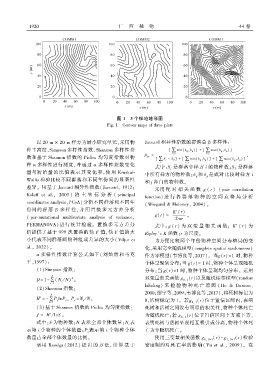
图 1 3 个样地地形图
Fig. 1 Contour maps of three plots
以 20 m × 20 m 样方为最小研究单元ꎬ采用物 Jaccard 相异性指数的群落总 β 多样性:
种丰富度、Simpson 多样性指数、Shannon 多样性指 [∑ min(b ij ꎬb ji )] + [∑ max(b ij ꎬb ji )]
i < j i < j
=
数和基于 Shannon 指数的 Pielou 均匀度指数对物 β jac ꎮ
[∑ S i - S T ] + [∑ min(b ij ꎬb ji )] + [∑ max(b ij ꎬb ji )]
i < j
i < j
i
种 α 多样性进行测度ꎬ并通过 α 多样性指数变化 式中:S 是群落中样方 i 的物种数ꎻS 是群落
i T
量与初始量的比值表示其变化率ꎬ使用 Kruskal ̄
中所有样方的物种数ꎻb 和 b 是成对比较时样方 i
ij
ji
Wallis 检验比较不同群落和不同年份间的显著性
和 j 各自的物种数ꎮ
差异ꎮ 用基于 Jaccard 相异性指数( Jaccardꎬ 1912ꎻ
采用 配 对 相 关 函 数 g ( r) ( pair correlation
Koleff et al.ꎬ 2003 ) 的 主 坐 标 分 析 ( principal function) 进 行 各 群 落 物 种 的 空 间 点 格 局 分 析
coordinates analysisꎬPCoA)分析不同群落和不同年
(Wiegand & Moloneyꎬ 2004)ꎮ
份间的 群 落 β 多 样 性ꎬ 并 用 置 换 多 元 方 差 分 析 K′(r)
g(r) = ꎮ
( per ̄mutational multivariate analysis of varianceꎬ 2πr
PERMANOVA) 进行统计检验ꎮ 置换多元方差分 式中: g ( r) 为 双 变 量 相 关 函 数ꎻ K′ ( r) 为
析提供了基于 999 次置换的伪 F 值ꎬ伪 F 值的大 Ripley’s K 函数ꎻr 为尺度ꎮ
小代表不同群落间物种组成差异的大小( Viljur et 为方便比较两个年份物种空间分布格局的变
al.ꎬ 2022)ꎮ 化ꎬ采用完全随机模型(complete spatial randomness)
α 多样性指数计算公式如下( 刘灿然和马克 作为零模型(韦博良等ꎬ2017)ꎮ 当g(r)>1 时ꎬ物种
平ꎬ1997): 个体呈聚集分布ꎻ当 g(r)= 1 时ꎬ物种个体呈现随机
(1)Simpson 指数: 分布ꎻ当 g(r)<1 时ꎬ物种个体呈现均匀分布ꎮ 运用
S
2 双变量相关函数 g (r)以及随机标签模型(random
D = 1-∑(N / N) ꎮ 0ꎬ 1
i
i = 1
labeling) 来 检 验 物 种 死 亡 原 因 ( He & Duncanꎬ
(2)Shannon 指数:
2000ꎻ缪宁等ꎬ2009ꎻ韦博良等ꎬ2017)ꎬ将死树标记为
S
H′ = -∑P lnP ꎬ P = N / Nꎮ 0ꎬ活树标记为 1ꎮ 若g (r) 位于置信区间内ꎬ表明
i
i
i
i
i = 1 0ꎬ 1
(3)基于 Shannon 指数的 Pielou 均匀度指数: 死树和活树之间没有明显的相关性ꎬ物种个体死亡
J = H′ / lnS ꎮ 为随机死亡ꎻ若 g (r) 位于置信区间上方或下方ꎬ
0ꎬ 1
式中:S 为物种数ꎻN 表示全部个体数量ꎻN 表 表明死树与活树呈现相互吸引或分离ꎬ物种个体死
i
示第 i 个物种的个体数量ꎻP 表示第 i 个物种个体 亡为非随机死亡ꎮ
i
数量占全部个体数量的比例ꎮ 使用三变量相关函数 g (r) -g (r) 检验
0ꎬ 0+1 1ꎬ 0+1
运用 Baselga ( 2012) 提 出 的 方 法ꎬ 计 算 基 于 密度制约对死亡率的影响( Yu et al.ꎬ 2009)ꎮ 在